If you are preparing for any competitive exams then you know to value of time. Saving even 10 sec per question can save you considerable amount of time to solve additional questions. In this article I’ll share the best square trick to quickly calculate the squares of numbers from 1 to 100.
What is square of a number ?
When any number is multiplied by itself, it is called as the square of the number.
Thus, 3 X 3 = 32 = 9
Role in Exams !
Squares have a very important role to play in the context of preparing for any aptitude exam. It might be a good idea to be able to recollect the squares of 2 digit numbers.
So let’s learn the square trick.
How to memorize ?
So, how does one get these numbers onto one’s finger tips? Does one memorize these values or is there a simpler way?
Yes indeed! There is a very convenient process when it comes to memorizing the squares of the first 100
numbers.
First of all, you are expected to memorize the squares of the first 30 numbers. In my experience, I have normally seen that most students already know this. The problem arises with numbers after 30. You do not need to worry about that.
I’ll divide the process into 4 Parts:
Part 1: Squares for number 1 to 30
(Toughest Part)
| Squares from 1 to 10 | Squares from 11 to 20 | Squares from 21 to 30 |
|---|---|---|
| 12 = 1 22 = 4 32 = 9 42 = 16 52 = 25 62 = 36 72 = 49 82 = 64 92 = 81 102 = 100 | 112 = 121 122 = 144 132 = 169 142 = 196 152 = 225 162 = 256 172 = 289 182 = 324 192 = 361 202 = 400 | 212 = 441 222 = 484 232 = 529 242 = 576 252 = 625 262 = 676 272 = 729 282 = 784 292 = 841 302 = 900 |
This is toughest because you have to do the hard part, that is memorizing. To improve your problem solving speed in exams you must remember squares up to 30. It should be at your finger tips. If you think this is all overwhelming then I have some good news. Practically you don’t need to memorize all 30 squares. Let me show you why.
Most of you should be comfortable with perfect squares up to 20.
So for remains 10 digits (21 – 30) you’ll have to memorize only first 5 digit. That is from 21 to 25. From these you can easily calculate the other half by just adding certain multiple of 100s.
Here’s how. Take a look at the pattern below!
Part 2: Squares for number 51 to 80
The process is best explained through an example.
Suppose, you have to get an answer for the value of 672. Look at 67 as (50 + 17). The 4 digit answer will have two parts as follows:
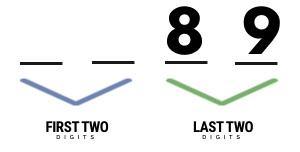
The last two digits will be the same as the last two digits of the square of the number 17. (The value 17 is derived by looking at the difference of 67 with respect to 50.)
Since, 172 = 289, you can say that the last two digits of 672 will be 89. (i.e. the last 2 digits of 289.) Also, you will need to carry over the ‘2’ in the hundreds place of 289 to the first part of the number.
The first two digits of the answer will be got by adding 17 (which is got from 67 – 50) and adding the carry over (2 in this case) to the number 25 (25 is standard number to be used in all cases). Hence, the first two digits of the answer will be given by:
25 + 17 + 2 = 44.
Hence, the answer is 672= 4489.
Similarly, suppose you have to find 762.
Step 1: 76 = 50 + 26.
Step 2: 262 is 676. Hence, the last 2 digits of the answer will be 76 and we will carry over 6.
Step 3: The first two digits of the answer will be 25 + 26 + 6 = 57.
Hence, the answer is 5776.
Part 3: Squares for number 31 to 50
Such numbers can be treated in the form (50 – x) and the above process modified to get the values of squares from 31 to 50. Again, to explain we will use an example. Suppose you have to find the square of 41.
Step 1: Look at 41 as (50 – 9).
Again, similar to what we did above, realize that the answer has two parts—the first two and the last two digits.
Step 2: The last two digits are got by the last two digits in the value of (– 9)2 = 81. Hence, 81 will represent the last two digits of 412.
Step 3: The first two digits are derived by 25 – 9 = 16 (where 25 is a standard number to be used in all cases and – 9 comes from the fact that (50 – 9) = 41).
Hence, the answer is 1681.
Note: In case there had been a carry over from the last two digits it would have been added to 16 to get the answer.
For example, in finding the value of 362 we look at 36 = (50 – 14)
Now, (–14)2 = 196. Hence, the last 2 digits of the answer will be 96. The number ‘1’ in the hundreds place will have to be carried over to the first 2 digits of the answer.
The, first two digits will be 25 – 14 + 1 = 12
Hence, 362 = 1296.
With this process, you are equipped to find the squares of numbers from 31 to 50.
Part 4: Squares for number 81 to 100
Suppose you have to find the value of 822. The following process will give you the answers.
Step 1: Look at 82 as (100 – 18). The answer will have 4 digits whose values will be got by focusing on getting the value of the last two digits and that of the first two digits.
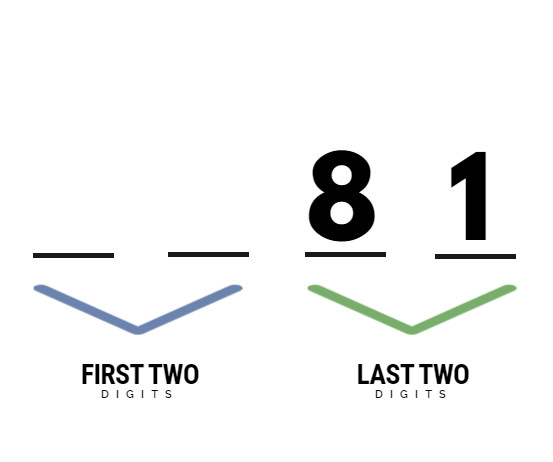
Step 2: The value of the last two digits will be equal to the last two digits of ( – 18)2.
Since, ( – 18)2 = 324, the last two digits of 822 will be 24. The ‘3’ in the hundreds place of (– 18)2 will be carried over to the other part of the answer (i.e. the first two digits).
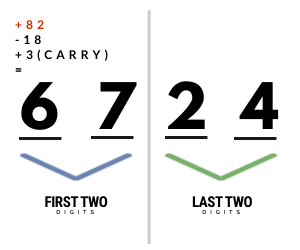
Step 3: The first two digits will be got by: 82 + (– 18) + 3 (Where 82 is the original number; (– 18) is the
number obtained by looking at 82 as (100 – x); and 3 is the carry over from (– 18)2).
Thus, the answer is 6724.
With these three processes you will be able to derive the square of any number up to 100.